Quadratwurzel

Die Quadratwurzel (umgangssprachlich Wurzel; englisch square root, kurz sqrt) einer nichtnegativen Zahl <math>y</math> ist jene (eindeutig bestimmte) nichtnegative Zahl, deren Quadrat gleich der gegebenen Zahl <math>y</math> ist. Das Symbol für die Quadratwurzel ist das Wurzelzeichen <math>\sqrt{}</math>, die Quadratwurzel der Zahl <math>y</math> wird also durch <math>\sqrt{y}</math> dargestellt. Dabei wird die Zahl beziehungsweise der Term <math>y</math> unter der Wurzel <math>\sqrt{y}</math> als Radikand bezeichnet. Weniger verbreitet ist die ausführlichere Schreibweise <math>\sqrt[2]{y}.</math> Außerdem kann man die Quadratwurzel als Potenz ausdrücken: <math>y^{\frac{1}{2}}</math> ist gleichwertig mit <math>\sqrt{y}.</math> Zum Beispiel ist wegen <math>3^2 = 3 \cdot 3 = 9</math> und <math>3\geq 0</math> die Quadratwurzel von <math>9</math> gleich <math>3</math>.
Da die Gleichung <math>x^2=y</math> für <math>y > 0</math> zwei Lösungen hat, definiert man üblicherweise die Quadratwurzel als die nichtnegative der beiden Lösungen, d. h., es gilt immer <math>\sqrt{y}\geq 0.</math> Damit erreicht man, dass der Begriff der Quadratwurzel eindeutig ist. Die beiden Lösungen der Gleichung sind somit <math>x_1=\sqrt{y}</math> und <math>x_2=-\sqrt{y}.</math>
Inhaltsverzeichnis
Vorbemerkung zu den Definitionen
Bei der formalen Definition der Quadratwurzel sind zwei Probleme zu berücksichtigen:
- Wenn man sich auf nichtnegative rationale Zahlen beschränkt, dann ist die Quadratwurzel in vielen Fällen nicht definiert. Schon in der Antike fand man heraus, dass etwa die Zahl <math>\sqrt{2}</math> keine rationale Zahl sein kann (siehe Euklids Beweis der Irrationalität der Wurzel aus 2).
- Im Allgemeinen existieren zwei verschiedene Zahlen, deren Quadrate mit einer vorgegebenen Zahl übereinstimmen. Beispielsweise wäre wegen <math>(-3)^2 = (-3) \cdot (-3) = 9</math> auch die Zahl <math>-3</math> ein möglicher Kandidat für die Quadratwurzel aus <math>9</math>.
Das Symbol für die Quadratwurzel wurde zum ersten Mal während des 16. Jahrhunderts benutzt. Es wird vermutet, dass das Zeichen eine modifizierte Form des kleinen r ist, das als Abkürzung für das lateinische Wort „radix“ (Wurzel) steht. Ursprünglich wurde das Symbol dem Radikanden vorangestellt; die waagerechte Verlängerung fehlte. Noch Carl Friedrich Gauß verwendete daher Klammern für kompliziertere Wurzelausdrücke und schrieb zum Beispiel <math>\sqrt{}(b^2-4ac)</math> anstelle von <math>\sqrt{b^2-4ac}.</math>
Im Englischen wird die Quadratwurzel als „square root“ bezeichnet, weshalb in vielen Programmiersprachen die Bezeichnung „sqrt“ für die Quadratwurzelfunktion verwendet wird.
Quadratwurzeln aus reellen Zahlen
Definition: Die Quadratwurzel <math>\sqrt{y}</math> einer nichtnegativen reellen Zahl <math>y</math> ist diejenige nichtnegative reelle Zahl <math>x</math>, deren Quadrat <math>x^2 = x \cdot x</math> gleich <math>y</math> ist.
Gleichwertig dazu kann die reelle Quadratwurzel als Funktion so definiert werden: Sei
- <math>\begin{align}
q\colon [0;\infty{[} &\rightarrow [0;\infty{[}\\
x&\mapsto y=x^2
\end{align}</math> die (bijektive) Einschränkung der Quadratfunktion auf die Menge der nichtnegativen reellen Zahlen. Die Umkehrfunktion dieser Funktion <math>q</math> heißt Quadratwurzelfunktion <math>y \mapsto x=\sqrt{y}.</math>
Bemerkungen
- Zu beachten ist, dass die durch <math>\mathbb{R}\rightarrow \mathbb{R}; x\mapsto x^2</math> erklärte Quadratfunktion für alle reellen Zahlen definiert, aber nicht umkehrbar ist. Sie ist weder injektiv noch surjektiv.
- Die Einschränkung <math>q</math> der Quadratfunktion ist umkehrbar und wird durch die reelle Wurzelfunktion umgekehrt. Da nur nichtnegative reelle Zahlen als Bilder von <math>q</math> auftreten, ist die reelle Wurzelfunktion nur für diese Zahlen definiert.
- Durch die vor der Umkehrung gemachte Einschränkung von <math>q</math> auf nichtnegative reelle Zahlen sind die Werte der Quadratwurzelfunktion nichtnegative Zahlen. Die Einschränkung der Quadratfunktion auf andere Teilmengen von <math>\mathbb{R}</math>, in denen verschiedene reelle Zahlen stets verschiedene Quadrate haben, würde zu anderen Umkehrfunktionen führen, diese werden aber nicht als reelle Quadratwurzelfunktion bezeichnet.
Beispiele
| Radikand | Quadratwurzel | Radikand | Quadratwurzel | |
|---|---|---|---|---|
| 1 | 1 | 121 | 11 | |
| 4 | 2 | 144 | 12 | |
| 9 | 3 | 169 | 13 | |
| 16 | 4 | 196 | 14 | |
| 25 | 5 | 225 | 15 | |
| 36 | 6 | 256 | 16 | |
| 49 | 7 | 289 | 17 | |
| 64 | 8 | 324 | 18 | |
| 81 | 9 | 361 | 19 | |
| 100 | 10 | 400 | 20 |
Eigenschaften und Rechenregeln
Die Eigenschaften der Quadratwurzelfunktion ergeben sich aus den Eigenschaften der auf die Menge der nichtnegativen reellen Zahlen eingeschränkten Quadratfunktion:
- <math>\sqrt{a\cdot b}=\sqrt{ a}\cdot\sqrt{ b}\;</math> für <math>\; 0\leq a, \, 0\leq b</math>.
- <math>\sqrt{a\cdot b}=\sqrt{-a}\cdot\sqrt{-b}\;</math> für <math>\; a\leq 0, \, b\leq 0</math>.
- <math>0\leq a<b \;\Longleftrightarrow\; 0\leq \sqrt{a}<\sqrt{b}</math>, d. h., die Quadratwurzelfunktion ist streng monoton wachsend.
- <math>\sqrt{a^2}=|a|</math> gilt mit dem reellen Betrag für beliebige reelle Zahlen <math>a</math>.
- Dagegen gilt <math>(\sqrt{a})^2=a</math> nur für nichtnegatives <math>a</math>.
- Die Quadratwurzelfunktion ist auf <math>\R_+</math> differenzierbar, dort gilt <math>\frac{\mathrm d\sqrt{x}}{\mathrm dx}=\frac{1}{2\sqrt{x}}</math>.
- An der Stelle 0 ist sie nicht differenzierbar, ihr Schaubild besitzt dort eine senkrechte Tangente mit der Gleichung <math>x=0</math>.
- Sie ist auf jedem abgeschlossenen Teilintervall <math>[a,b]</math> ihres Definitionsbereichs Riemann-integrierbar, eine ihrer Stammfunktionen ist <math>F(x)=\tfrac{2}{3}\cdot \sqrt{x^3}</math>.
Berechnung von Quadratwurzeln aus reellen Zahlen
| Rationale (Näherungs-) Werte einiger Quadratwurzeln |
|---|
| <math>\begin{array}{ccccr}
\sqrt2&\approx&\sqrt{\frac{49}{25} }&=&\frac75\\ \sqrt2&\approx&\sqrt{\frac{289}{144} }&=&\frac{17}{12}\\ \sqrt2&\approx&\sqrt{\frac{100}{49} }&=&\frac{10}{7}\\ \sqrt3&\approx&\sqrt{\frac{49}{16} }&=&\frac74\\ \sqrt4&&&=&2\\ \sqrt5&\approx&\sqrt{\frac{81}{16} }&=&\frac94\\ \sqrt6&\approx&\sqrt{\frac{2401}{400} }&=&\frac{49}{20}\\ \sqrt7&\approx&\sqrt{\frac{64}{9} }&=&\frac{8}{3}\\ \sqrt8&\approx&\sqrt{\frac{289}{36} }&=&\frac{17}{6}\\ \sqrt9&&&=&3\\ \sqrt{10}&\approx&\sqrt{\frac{361}{36} }&=&\frac{19}{6}\\ \sqrt{11}&\approx&\sqrt{\frac{100}{9} }&=&\frac{10}{3} \end{array}</math> |
Selbst dann, wenn die Quadratwurzel aus einer natürlichen Zahl gezogen werden soll, ist das Ergebnis häufig eine irrationale Zahl, deren Dezimalbruchentwicklung also ein nichtperiodischer, nicht abbrechender Dezimalbruch ist (nämlich genau dann, wenn das Ergebnis nicht natürlich ist). Die Berechnung einer Quadratwurzel, die keine rationale Zahl ist, besteht also darin, einen Näherungswert ausreichender Genauigkeit zu bestimmen. Dazu gibt es eine Reihe von Möglichkeiten:
- Schriftliches Wurzelziehen
- Hierbei handelt es sich um einen Algorithmus ähnlich dem gängigen Verfahren der schriftlichen Division.
- Intervallschachtelung
- Dieses Verfahren ist recht leicht zu verstehen, wenn auch in der praktischen Durchführung sehr mühsam.
- Beispiel (Näherungswert für <math>\sqrt{2}</math>):
- Aus <math>1^2 = 1 < 2</math> und <math>2^2 = 4 > 2</math> folgt, dass <math>\sqrt{2}</math> zwischen 1 und 2 liegt. Daher probiert man <math>1{,}1^2</math>, <math>1{,}2^2</math> usw. durch. Aus <math>1{,}4^2 = 1{,}96 < 2</math> und <math>1{,}5^2 = 2{,}25 > 2</math> erkennt man, dass <math>\sqrt{2}</math> zwischen 1,4 und 1,5 liegen muss. Fortsetzung dieses Verfahrens mit immer mehr Nachkommastellen liefert schließlich einen Näherungswert mit der gewünschten Genauigkeit:
- <math>1{,}41421356^2<2<1{,}41421357^2\;\Rightarrow\;\sqrt{2}\approx 1{,}41421356</math>
- Babylonisches Wurzelziehen oder Heron-Verfahren
- Dieses Iterationsverfahren wird häufig bei der Programmierung der Wurzelberechnung für Taschenrechner verwendet, da es schnell konvergiert. Es handelt sich um das Newton-Verfahren zum Auffinden von Nullstellen, angewandt auf die Funktion <math>x\mapsto x^2-a</math>.
- Taylorreihen-Entwicklung
- Die Taylorreihen-Entwicklung der Wurzelfunktion <math>t\mapsto \sqrt{t}</math> mit Entwicklungsstelle <math>t = 1</math> kann als Taylor-Entwicklung von <math>x\mapsto (1+x)^{1/2}</math> um die Stelle <math>x = 0</math> als binomische Reihe
- <math>\sum_{n=0}^\infty \binom{1/2}{n}\,x^n = \sum_{n=0}^\infty \binom{2n}{n}\,\frac{(-1)^{n+1}}{(2n-1)\, 4^n}\,x^n = 1 + \frac{1}{2} x - \frac{1}{8} x^2 + \frac{1}{16} x^3 - \frac{5}{128} x^4 \pm \dotsb</math>
- gefunden werden, weil diese Reihe für <math>|x| \leq 1</math> punktweise gegen <math>\sqrt{1+x}</math> konvergiert. Mit <math>x := t-1</math> ergibt das
- <math>\sqrt{t}=1 + \frac{1}{2} (t-1) - \frac{1}{8} (t-1)^2 + \frac{1}{16} (t-1)^3 - \frac{5}{128} (t-1)^4 \pm \dotsb</math> für <math>0 \leq t \leq 2.</math>
- Berechnung mittels CORDIC-Algorithmus
- Dieses Verfahren wird vor allem in Rechenwerken, FPUs und Mikrocontrollern eingesetzt.
Ermittlung der Quadratwurzel auf grafischem Wege
Eine Möglichkeit bietet der Kathetensatz: Die Zahl <math>n</math>, deren Quadratwurzel gesucht ist, wird auf einer Zahlengeraden von <math>0</math> aus aufgetragen. Über der Strecke zwischen <math>0</math> und <math>n</math> wird ein Halbkreis mit Radius <math>r=\tfrac{n}{2}</math> gezeichnet (Thaleskreis). Bei <math>1</math> wird ein Lot zur Grundlinie errichtet, das den Halbkreis schneidet (Höhe eines rechtwinkligen Dreiecks). Der Abstand dieses Schnittpunkts zum Nullpunkt ist die Quadratwurzel von <math>n</math> (Kathete).
Quadratwurzeln aus komplexen Zahlen
Ist <math>z</math> eine von Null verschiedene komplexe Zahl, so besitzt die Gleichung
- <math>w^2 = z</math>
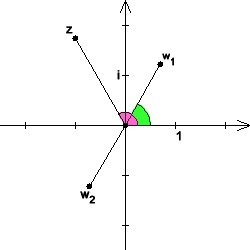
genau zwei Lösungen für <math>w</math>, die man auch als Wurzeln oder Quadratwurzeln von <math>z</math> bezeichnet. Diese liegen in der Gaußschen Zahlenebene auf den beiden Schnittpunkten des Kreises um 0 mit dem Radius <math>\sqrt{|z|}</math> und der Winkelhalbierenden des Winkels zwischen den von <math>0</math> ausgehenden Strahlen durch <math>1</math> bzw. <math>z</math>. Diejenige der beiden Wurzeln, die in der rechten Halbebene liegt, nennt man den Hauptwert (engl. principal value) der Wurzel. Für negatives (reelles) <math>z</math> ist die Wurzel mit positivem Imaginärteil der Hauptwert.
Schreibt man die komplexe Zahl <math>z</math> in der Form
- <math>z=r\cdot \rm e^{\mathrm i\varphi},</math>
wobei <math>\varphi</math> und <math>r</math> reell sind mit <math>r > 0</math> und <math>-\pi < \varphi \le \pi</math>, so gilt für den Hauptwert der Wurzel:
- <math>w_1=\sqrt{r}\cdot \rm e^{\mathrm i\varphi/2}</math>
Der zweite Wurzelwert (der Nebenwert) ergibt sich durch Punktspiegelung (180°-Drehung) am Nullpunkt:
- <math>w_2 = \sqrt{r} \cdot \rm e^{\mathrm i (\varphi / 2 + \pi)}</math>
Definition
Die komplexe Funktion „Quadriere z“, <math>q\colon \mathbb{C}\rightarrow \mathbb{C}; z\mapsto z^2</math> besitzt genau wie die reelle Quadratfunktion keine Umkehrfunktion, denn sie ist nicht injektiv, aber im Gegensatz zu den reellen Zahlen surjektiv, das heißt, jede komplexe Zahl ist das Quadrat einer komplexen Zahl. Man kann daher analog zu den reellen (nichtnegativen) Quadratwurzeln komplexe Quadratwurzelfunktionen definieren, indem man eine Einschränkung des Definitionsbereichs von <math>q</math> auf eine Teilmenge <math>D</math> der komplexen Zahlen vornimmt, auf der <math>q</math> injektiv ist und surjektiv bleibt. Je nachdem, welche Teilmenge man dafür auswählt, erhält man als Umkehrung unterschiedliche Zweige der Quadratwurzelfunktion.
Der Hauptzweig der komplexen Quadratwurzelfunktion ergibt sich, wenn man als Definitionsbereich von <math>q</math>
- <math> D_H:=\{x+ \mathrm i\, y\in\mathbb{C} \mid x>0 \text{ oder } (x=0 \text{ und } y\geq 0)\}</math>
zugrunde legt, dies ist die rechte Halbebene der komplexen Zahlenebene, wobei von deren Rand nur die Zahlen mit nichtnegativem Imaginärteil zu <math>D_H</math> gehören. Die Einschränkung von <math>q</math> auf <math>D_H</math> ist eine bijektive Abbildung von <math>D_H</math> auf die komplexen Zahlen, daher ist ihre Umkehrfunktion, der Hauptzweig der Quadratwurzel auf ganz <math>\C</math> definiert. Den Wert <math>\sqrt{z}</math> dieser Umkehrfunktion nennt man den Hauptwert der Quadratwurzel von <math>z</math>. Wenn mit <math>\sqrt{z}</math> eine bestimmte komplexe Zahl gemeint ist, dann ist es dieser Hauptwert.
Ist <math>z</math> in kartesischen Koordinaten gegeben, also <math>z=x+\rm iy</math> mit reellen Zahlen <math>x</math> und <math>y</math>, dann ergibt sich
- <math>
\sqrt{z} = \sqrt{x+\rm iy} = \sqrt{\tfrac{|z|+x}{2}} + \mathrm i\cdot \operatorname{sgn^+}(y) \cdot\sqrt{\tfrac{|z|-x}{2}} </math> für den Hauptwert der Quadratwurzel, wobei die Funktion <math>\operatorname{sgn^+}</math> für negative <math>y</math> den Wert −1 und ansonsten (also auch für <math>y=0</math> und damit anders als bei der Vorzeichenfunktion <math>\operatorname{sgn}</math>) den Wert 1 hat:
- <math>\text{sgn}^+(y)=\begin{cases} +1&\text{ für } y\ge 0\\ -1&\text{ für } y<0 \end{cases}</math>
Der einzige Nebenzweig von <math>q</math> ist <math>-\sqrt{z}.</math>
Ist <math>z</math> in Polarkoordinaten gegeben, <math>z=|z| \cdot \mathrm e^{\mathrm i\cdot \arg(z)}</math> mit <math>\arg(z) \in (-\pi,\pi]</math>, dann ist der Hauptwert der Quadratwurzel durch
- <math>\sqrt{z} = \sqrt{|z|} \mathrm e^{\mathrm i \cdot \arg(z)/2}</math>
gegeben, wobei <math>\sqrt{|z|}</math> die reelle (nichtnegative) Quadratwurzel von <math>|z|</math> ist. Der Nebenwert ergibt sich wieder als <math>-\sqrt{z} = \sqrt{|z|} \mathrm e^{\mathrm i \cdot (\arg(z)/2 +\pi)}</math>.
Der Betrag der beiden Wurzeln ergibt sich demnach als die Wurzel aus dem Betrag der komplexen Zahl. Beim Hauptwert wird das Argument <math>\arg(z)</math> („der Winkel von z“, s. u.) halbiert. Die andere Lösung ergibt sich geometrisch durch Punktspiegelung dieses Hauptwerts am Ursprung.
Das Argument einer komplexen Zahl <math>z=x+\mathrm i\, y</math> ist der orientierte Winkel <math>\angle(EOZ)</math> in der komplexen Zahlenebene, die Punkte sind <math>E(1|0),</math> <math>O(0|0)</math> und <math>Z(x|y)</math> in reellen Koordinaten. Im Bild zum folgenden Beispiel sind das Argument von <math>z</math> und das Argument von <math>w_1</math> farbig gekennzeichnet.
- Komplexe Quadratwurzel
Die Riemannsche Fläche der Quadratwurzel lässt erkennen, wie die beiden Zweige ineinander übergehen.
Beispiel: Berechnung einer komplexen Quadratwurzel
Gesucht sind die Quadratwurzeln aus <math>z = -1+\mathrm i\,\sqrt{3}.</math> Zunächst wird der Betrag des Radikanden ermittelt:
- <math>|z| = \left|-1+\mathrm i\sqrt{3} \right| = \sqrt{(-1)^2 + (\sqrt{3})^2} = \sqrt{1+3} = \sqrt{4} = 2</math>
Damit ergibt sich der Hauptwert der Quadratwurzel zu
- <math>\begin{align}
w_1 &= \sqrt{\tfrac{2+(-1)}{2}}
+ \mathrm i \cdot \operatorname{sgn^+}(\sqrt{3}) \cdot \sqrt{\tfrac{2-(-1)}{2}}
\\[0.3em] &= \sqrt{\tfrac{1}{2}} + \mathrm i \cdot (+1) \cdot \sqrt{\tfrac{3}{2}} = \sqrt{2} \cdot \left(\tfrac{1}{2} + \mathrm i \cdot \tfrac{1}{2}\sqrt{3} \right) \end{align}</math> Die andere Wurzel erhält man durch Vorzeichenumkehr:
- <math>w_2 = -w_1 = \sqrt{2} \cdot \left( -\tfrac{1}{2} - \mathrm i \cdot \tfrac{1}{2}\sqrt{3} \right)</math>
Potenzgesetz
Das Potenzgesetz
- <math>
(a\cdot b)^r = a^r\cdot b^r \qquad \qquad \qquad \qquad \qquad \qquad \quad \text{(P)}
</math>
gilt bei <math>r=1/2</math> nicht für alle <math>a, b \in \C</math>, auch nicht für die Hauptwerte der Wurzeln.
Das sieht man schon an dem sich durch die weitere Spezifizierung <math>a=b=:z</math> ergebenden Spezialfall
- <math>\sqrt{z^2} = \left(\sqrt{z}\right)^2,</math>
der sich wegen der Identität <math>\left(\sqrt{z}\right)^2=z</math> zu
- <math>\sqrt{z^2} = z</math>
vereinfachen lässt, wonach offenbar schon jede negative Zahl ein Gegenbeispiel liefert, etwa <math>z=-1</math>:
- Wegen <math>(-1)^2 = 1</math> und <math>\arg(1) = 0</math> hat der Hauptwert von <math>\sqrt{(-1)^2}</math> das Argument <math>\arg(\sqrt{1}) = 0/2 = 0</math>, während der Hauptwert von <math>-1</math> das Argument <math>\arg(-1) = \pi</math> hat.[1]
- Bemerkungen
- Da Hauptwerte von Wurzeln aus positiven Radikanden positiv sein müssen, zeigt das Gegenbeispiel, dass es eine Quadratwurzelfunktion, für die das Potenzgesetz <math>\text{(P)}</math> für alle <math>a, b \in \C</math> gilt, nicht geben kann.
- Für <math>r=1/2</math> und beliebige <math>a, b \in \C</math> kann man in <math>\text{(P)}</math> die „Vorzeichen“ von zwei der drei Wurzeln frei wählen, wonach genau eine Möglichkeit für das „Vorzeichen“ der letzten dritten übrig bleibt.
Quadratwurzeln modulo n
Auch im Restklassenring <math>\mathbb{Z} / n \mathbb{Z}</math> lassen sich Quadratwurzeln definieren. Ganz analog zu den reellen und komplexen Zahlen heißt <math>q</math> eine Quadratwurzel von <math>x</math>, wenn gilt:
- <math>q^2 \equiv x \bmod n</math>
Allerdings muss man sich zur Berechnung von Quadratwurzeln modulo <math>n</math> anderer Methoden bedienen als beim Berechnen reeller oder komplexer Quadratwurzeln. Um die Quadratwurzeln von <math>x</math> modulo <math>n</math> zu bestimmen, kann man folgendermaßen vorgehen:
Zuerst bestimmt man die Primfaktorzerlegung
- <math>n = p_1^{m_1} \cdot p_2^{m_2} \dotsm p_{k}^{m_k}</math>
des Moduls <math>n</math> und anschließend die Lösungen modulo der einzelnen Primzahlpotenzen <math>p^m</math>. Diese Lösungen setzt man schließlich unter Anwendung des Chinesischen Restsatzes zur gesuchten Lösung zusammen.
Berechnung von Quadratwurzeln modulo einer Primzahl p
Der Fall <math>p=2</math> ist einfach: Wegen <math>0^2=0, \, 1^2=1</math> und <math>1 \not \equiv 0 \bmod 2</math> hat modulo 2 jede Zahl eine eindeutig bestimmte Quadratwurzel, nämlich sich selbst. Für Primzahlen <math>p</math> ungleich 2 geschieht das Berechnen der Quadratwurzeln von <math>x</math> so:
Um zu testen, ob <math>x</math> überhaupt eine Quadratwurzel in <math>\mathbb Z/p \mathbb Z</math> hat, berechnet man den Wert des Legendre-Symbols
- <math>\left(\frac xp\right) \equiv x^{\frac{p-1}2} \bmod p</math>,
denn es gilt:
- <math>
\left(\frac xp\right) = \begin{cases}
-1, & \text{wenn }x \text{ quadratischer Nichtrest modulo }p \text{ ist}\\
0, & \text{wenn }x \text{ und }p \text{ nicht teilerfremd sind }\\
1, & \text{wenn }x \text{ ein quadratischer Rest modulo }p \text{ ist}
\end{cases}</math> Im ersten Falle besitzt <math>x</math> keine Quadratwurzel in <math>\mathbb Z/p \mathbb Z</math> und im zweiten Fall nur die Quadratwurzel 0. Der interessante Fall ist also der dritte Fall, und daher nehmen wir im Folgenden an, dass <math>\bigl(\tfrac{x}{p}\bigr) = 1</math> gilt.
Berechnung für den Fall p mod 4 = 3
Ist das Legendre-Symbol <math>\bigl(\tfrac{x}{p}\bigr)</math> gleich 1, dann sind
- <math>q \equiv \pm x^{\frac{p+1}{4}} \bmod p </math>
die beiden Quadratwurzeln von <math>x</math> modulo <math>p</math>.
Berechnung für den Fall p mod 4 = 1
Ist das Legendre-Symbol <math>\bigl(\tfrac{x}{p}\bigr)</math> gleich 1, dann sind
- <math>q \equiv \pm \frac{x}{2r}\left(W_\frac{p-1}{4} + W_\frac{p+3}{4} \right) \bmod p</math>
die beiden Quadratwurzeln von <math>x</math> modulo <math>p</math>. Hierbei wählt man <math>r</math> so, dass
- <math>\left(\frac{r^2-4x}{p}\right) = -1</math>
gilt. Dazu kann man einfach verschiedene Werte von <math>r</math> testen. Die Folge <math>W_n</math> ist rekursiv durch
- <math>
W_n = \begin{cases} r^2/x-2, & \text{ wenn }n = 1\\ W_{n/2}^2-2, & \text{ wenn }n \text{ gerade}\\ W_{(n+1)/2}W_{(n-1)/2}-W_1, & \text{ wenn }n > 1 \text{ ungerade} \end{cases} </math> definiert.
Rechenbeispiel für <math>x=3</math> und <math>p=37</math>:
Nach obiger Formel sind die Quadratwurzeln von <math>x</math> durch
- <math>q \equiv \pm \frac{x}{2r}\left(W_9 + W_{10} \right) \bmod 37</math>
gegeben. Für <math>r</math> findet man durch Probieren den Wert <math>r = 2</math>, denn es gilt:
- <math>
\left(\frac{r^2-4x}{p}\right) \equiv (r^2-4x)^\frac{p-1}2 \equiv (-8)^{18} \equiv 36 \equiv -1 \bmod 37 </math> Die Werte für <math>W_9</math> und <math>W_{10}</math> ergeben sich so:
- <math>\begin{matrix}
W_1 &\equiv& r^2/x-2 &\equiv& 4/3-2 &\equiv& 24 & \bmod 37 \\ W_2 &\equiv& W_1^2-2 &\equiv& 24^2-2 &\equiv& 19 & \bmod 37 \\ W_3 &\equiv& W_1 W_2 - W_1 &\equiv& 24\cdot 19 - 24 &\equiv& 25 & \bmod 37 \\ W_4 &\equiv& W_2^2-2 &\equiv& 19^2-2 &\equiv& 26 & \bmod 37 \\ W_5 &\equiv& W_2 W_3 - W_1 &\equiv& 19\cdot 25 - 24 &\equiv& 7 & \bmod 37 \\ W_9 &\equiv& W_4 W_5 - W_1 &\equiv& 26\cdot 7 - 24 &\equiv& 10 & \bmod 37 \\ W_{10}&\equiv& W_5^2-2 &\equiv& 7^2-2 &\equiv& 10 & \bmod 37 \\ \end{matrix}</math> Einsetzen dieser Werte ergibt
- <math>
q \equiv \pm \frac{x}{2r}\left(W_9 + W_{10} \right)
\equiv \pm \frac{3}{4}(10 + 10)
\equiv \pm 15 \bmod 37. </math> Das heißt: 15 und 22 sind die beiden Quadratwurzeln von 3 modulo 37.
Quadratwurzeln aus Matrizen
Als Wurzel einer quadratischen Matrix <math>A</math> bezeichnet man alle Matrizen <math>B</math>, die mit sich selbst multipliziert <math>A</math> ergeben:
- <math>A = B\cdot B \Leftrightarrow B \text{ ist Wurzel von } A</math>
Wie schon bei der Wurzel aus reellen oder komplexen Zahlen ist die Wurzel aus Matrizen nicht unbedingt eindeutig. Betrachtet man aber nur positiv definite symmetrische Matrizen, so ist die Wurzelbildung eindeutig: Jede positiv definite symmetrische Matrix <math>A</math> besitzt eine eindeutig bestimmte positiv definite symmetrische Wurzel <math>A^\frac{1}{2}.</math> Man erhält sie, indem man <math>A</math> mithilfe einer orthogonalen Matrix diagonalisiert (dies ist nach dem Spektralsatz stets möglich) und dann die Diagonalelemente durch ihre Wurzeln ersetzt; dabei ist jedoch stets die positive Wurzel zu wählen. Siehe auch Cholesky-Zerlegung. Die Eindeutigkeit folgt daraus, dass die Exponentialabbildung ein Diffeomorphismus vom Vektorraum der symmetrischen Matrizen auf die Teilmenge der positiv definiten symmetrischen Matrizen ist.
Quadratwurzel aus einem genäherten Integraloperator
Man kann die bestimmte Integral-Funktion <math>G, \, g_i:=g(x_i)</math> von 0 bis <math>x_i</math> mit <math>x_i=i\Delta x </math> und <math>i = 0, 1, \dotsc, n-1</math> einer vorgegebenen Funktion <math>F, \, f_i:=f(x_i)</math>, die an den äquidistanten Stützstellen <math>x_i</math> die Werte <math>f_i</math> annimmt, als Matrizenmultiplikation <math>G=FI</math> wie folgt numerisch nähern (für <math>n=4</math>):
- <math>
G = F I = \begin{pmatrix}
g_0 & g_1 & g_2 & g_3 \\
0 & g_0 & g_1 & g_2 \\
0 & 0 & g_0 & g_1 \\
0 & 0 & 0 & g_0
\end{pmatrix}
=
\begin{pmatrix}
f_0 & f_1 & f_2 & f_3 \\
0 & f_0 & f_1 & f_2 \\
0 & 0 & f_0 & f_1 \\
0 & 0 & 0 & f_0
\end{pmatrix} \begin{pmatrix}
\Delta x & \Delta x & \Delta x & \Delta x \\
0 & \Delta x & \Delta x & \Delta x \\
0 & 0 & \Delta x & \Delta x \\
0 & 0 & 0 & \Delta x
\end{pmatrix} </math> Es ist anschaulich klar, dass man diese Operation wiederholen kann und damit das Doppelintegral <math>H, \, h_i:=h(x_i)</math> erhält:
- <math>H = G I = F I I = F I^2</math>
So kann man die Matrix <math>I</math> als numerisch genäherten Integraloperator auffassen.
Die Matrix <math>I</math> ist nicht diagonalisierbar und ihre jordansche Normalform lautet:
- <math>
\begin{pmatrix}
\Delta x & 1 & 0 & 0 \\
0 & \Delta x & 1 & 0 \\
0 & 0 & \Delta x & 1 \\
0 & 0 & 0 & \Delta x
\end{pmatrix} </math>
Um eine Quadratwurzel daraus zu ziehen, könnte man so vorgehen wie bei den nicht diagonalisierbaren Matrizen beschrieben. Es gibt jedoch in diesem Fall eine direktere formale Lösung wie folgt:
- <math>
I^\beta =
\begin{pmatrix}
\alpha_0 & \alpha_1 & \alpha_2 & \alpha_3 \\
0 & \alpha_0 & \alpha_1 & \alpha_2 \\
0 & 0 & \alpha_0 & \alpha_1 \\
0 & 0 & 0 & \alpha_0
\end{pmatrix}
</math> mit <math>\alpha_0 = (\Delta x)^\beta</math>, <math>\alpha_k=\sum_{j=1}^{k} \frac{\Gamma(\beta + 1)(-1)^{j+1}\alpha_{k-j}} {\Gamma(j+1)\Gamma(\beta-j+1)}</math> und <math>k=1, 2, \dotsc, n-1</math>.
Darin bezeichnen die Indizes von <math>\alpha</math> die Subdiagonalen (0 ist die Diagonale) und der Exponent <math>\beta</math> ist gleich <math>\tfrac{1}{2}</math>. Setzt man <math>\Delta x</math> als reell und positiv voraus, so ist <math>(\Delta x)^\frac{1}{2}</math> reell und definitionsgemäß positiv.
Damit kann man ein „halbes“ bestimmtes Integral <math>L, \, l_i:=l(x_i)</math> von 0 bis <math>x_i</math> der Funktion <math>f(x)</math> wie folgt numerisch nähern:
- <math>
L = F I^\beta = \begin{pmatrix}
l_0 & l_1 & l_2 & l_3 \\
0 & l_0 & l_1 & l_2 \\
0 & 0 & l_0 & l_1 \\
0 & 0 & 0 & l_0
\end{pmatrix}
=
\begin{pmatrix}
f_0 & f_1 & f_2 & f_3 \\
0 & f_0 & f_1 & f_2 \\
0 & 0 & f_0 & f_1 \\
0 & 0 & 0 & f_0
\end{pmatrix} \begin{pmatrix}
\alpha_0 & \alpha_1 & \alpha_2 & \alpha_3 \\
0 & \alpha_0 & \alpha_1 & \alpha_2 \\
0 & 0 & \alpha_0 & \alpha_1 \\
0 & 0 & 0 & \alpha_0
\end{pmatrix} </math> Sucht man alle Operatoren, die mit sich selbst multipliziert den angenäherten Integraloperator <math>I</math> ergeben, so muss man zusätzlich das negative Vorzeichen einsetzen, das heißt, es gibt zwei Lösungen <math>\pm I^\frac{1}{2}</math>.
Zum Herleiten der Formel kann man zunächst <math>I</math> invertieren, das Resultat mit <math>\beta</math> potenzieren und zuletzt nochmals invertieren.
Siehe auch
Externe Links
Einzelnachweise
- ↑ Die Gültigkeit des Potenzgesetzes <math>\text{(P)}</math> für Quadratwurzeln wird an der zitierten Stelle nicht, aber gelegentlich in der Literatur (für negative reelle Radikanden) unterstellt: Klaus Fritzsche: Tutorium Mathematik für Einsteiger. Springer-Verlag, 2016, ISBN 978-3-662-48910-9 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 4. Juli 2017]).