Primzahl

<math>\mathbb P</math>

Eine Primzahl (wörtlich „erste Zahl“ oder eher „Zahl erster Klasse“) ist eine natürliche Zahl, die größer als 1 und ausschließlich durch sich selbst und durch 1 teilbar ist. Die Primzahlen sind damit innerhalb der Menge <math>\N</math> der natürlichen Zahlen dadurch charakterisiert, dass jede von ihnen genau zwei natürliche Zahlen als Teiler hat. Die aus allen Primzahlen bestehende Teilmenge von <math>\N</math> wird in der Regel mit dem Symbol <math>\mathbb P</math> bezeichnet.

Unmittelbar mit <math>\mathbb P</math> verknüpft ist die Folge <math>\left(p_n \right)_{n \in \N}</math> der nach ihrer Größe geordneten Primzahlen, die man auch kurz die Primzahlfolge nennt. Es ist demnach

<math>\N \supsetneq \mathbb P = \{ p_n \mid n \in \N \}</math>

mit

<math>\left(p_n \right)_{n \in \N} = \left( 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, \dotsc \right)</math> (Vorlage:OEIS).

Die Zahl 12 ist keine Primzahl, die Zahl 11 hingegen schon.

Eine natürliche Zahl ist prim, wenn sie eine Primzahl ist. Andernfalls ist sie zusammengesetzt. Die Zahlen 0 und 1 sind weder prim noch zusammengesetzt.

Das Wort „Primzahl“ kommt aus dem Lateinischen (numerus primus) und bedeutet „die erste Zahl“. Die Bedeutung der Primzahlen <math>\mathbb P</math> für viele Bereiche der Mathematik beruht auf drei Folgerungen aus dieser Definition:

• Existenz und Eindeutigkeit der Primfaktorzerlegung: Jede natürliche Zahl, die größer als 1 und selbst keine Primzahl ist, lässt sich als Produkt von mindestens zwei Primzahlen schreiben. Diese Produktdarstellung ist bis auf die Reihenfolge der Faktoren eindeutig. Zum Beweis dient das
• Lemma von Euklid: Ist ein Produkt zweier natürlicher Zahlen durch eine Primzahl teilbar, so ist mindestens einer der Faktoren durch sie teilbar.
• Primzahlen lassen sich nicht als Produkt zweier natürlicher Zahlen, die beide größer als 1 sind, darstellen.

Diese Eigenschaften werden in der Algebra für Verallgemeinerungen des Primzahlbegriffs genutzt.

Schon im antiken Griechenland interessierte man sich für die Primzahlen und entdeckte einige ihrer Eigenschaften. Obwohl Primzahlen seit damals stets einen großen Reiz auf die Menschen ausübten, sind viele die Primzahlen betreffenden Fragen bis heute ungeklärt, darunter solche, die mehr als hundert Jahre alt und leicht verständlich formulierbar sind. Dazu gehören die Goldbachsche Vermutung, wonach außer 2 jede gerade Zahl als Summe zweier Primzahlen darstellbar ist, und die Vermutung, dass es unendlich viele Primzahlzwillinge gibt (das sind Paare von Primzahlen, deren Differenz gleich 2 ist).

Über 2000 Jahre lang konnte man keinen praktischen Nutzen aus dem Wissen über die Primzahlen ziehen. Dies änderte sich erst mit dem Aufkommen elektronischer Rechenmaschinen, bei denen die Primzahlen beispielsweise in der Kryptographie eine zentrale Rolle spielen.

Primfaktorzerlegung

Es gilt der Fundamentalsatz der Arithmetik: Jede positive ganze Zahl lässt sich als (ggf. leeres) Produkt von Primzahlen darstellen, und diese Darstellung ist bis auf die Reihenfolge der Primzahlen eindeutig. Diese Primzahlen nennt man die Primfaktoren der Zahl. Man kennt bisher keine Methode, um die Primfaktorzerlegung einer beliebigen gegebenen Zahl effizient zu bestimmen, d. h. in einer Zeit, die polynomiell mit der Länge der Zahl wächst. Die Faktorisierungsannahme besagt, dass es eine solche Methode auch nicht gibt. Man versucht, die Zeit mit geeigneten Faktorisierungsverfahren zu minimieren.

Aufgrund dieses Satzes, also dass sich jede natürliche Zahl größer 0 durch Multiplikation von Primzahlen eindeutig darstellen lässt, nehmen die Primzahlen eine besondere atomare Stellung in der Mathematik ein. Alexander K. Dewdney bezeichnete diese als den Elementen der Chemie weitgehend ähnlich.

Eigenschaften von Primzahlen

Mit Ausnahme der Zahl 2 sind alle Primzahlen <math>p</math> ungerade, denn alle größeren geraden Zahlen lassen sich außer durch sich selbst und 1 auch noch (mindestens) durch 2 teilen. Damit hat jede Primzahl außer 2 die Form <math>2k+1</math> mit einer natürlichen Zahl <math>k</math>.

Jede Primzahl <math>p \neq 2</math> lässt sich einer der beiden Klassen „Primzahl der Form <math>4k+1</math>“ oder „Primzahl der Form <math>4k+3</math>“ zuordnen, wobei <math>k</math> eine natürliche Zahl ist. Darüber hinaus hat jede Primzahl <math>p > 3</math> die Form <math>p = 6k+1</math> oder <math>p = 6k-1</math>, wobei <math>k</math> eine natürliche Zahl ist. Nach dem dirichletschen Primzahlsatz gibt es in jeder dieser vier Klassen unendlich viele Primzahlen.

Jede natürliche Zahl der Form <math>4m+3</math> mit einer nichtnegativen ganzen Zahl <math>m</math> enthält mindestens einen Primfaktor der Form <math>4k+3</math>. Eine entsprechende Aussage über Zahlen der Form <math>4m+1</math> oder Primfaktoren der Form <math>4k+1</math> ist nicht möglich.

Eine Primzahl <math>p>2</math> lässt sich genau dann in der Form <math>a^2+b^2</math> mit ganzen Zahlen <math>a,b</math> schreiben, wenn <math>p</math> die Form <math>4k+1</math> hat. In diesem Fall ist die Darstellung im Wesentlichen eindeutig, d. h. bis auf Reihenfolge und Vorzeichen von <math>a,b</math>. Diese Darstellung entspricht der Primfaktorzerlegung

<math>p=(a+b\mathrm i)(a-b\mathrm i)</math>

im Ring der ganzen gaußschen Zahlen.

Die Zahl −1 ist ein quadratischer Rest modulo jeder Primzahl der Form <math>4k+1</math> und quadratischer Nichtrest modulo jeder Primzahl der Form <math>4k+3</math>.

Der kleine Satz von Fermat

Es sei <math>p</math> eine Primzahl. Für jede ganze Zahl <math>a</math>, die nicht durch <math>p</math> teilbar ist, gilt (für die Notation siehe Kongruenz):

<math>a^{p-1} \equiv 1 \mod p.</math>

Für nicht durch <math>p</math> teilbare Zahlen <math>a</math> ist die folgende Formulierung äquivalent:

<math>a^p\equiv a\mod p.</math>

Es gibt Zahlen, die keine Primzahlen sind, sich aber dennoch zu einer Basis <math>a</math> wie Primzahlen verhalten und somit den kleinen Satz von Fermat erfüllen. Solche zusammengesetzten Zahlen nennt man fermatsche Pseudoprimzahlen zur Basis <math>a</math>. Eine fermatsche Pseudoprimzahl n, die pseudoprim bezüglich aller zu ihr teilerfremden Basen <math>a</math> ist, nennt man Carmichael-Zahl.

In diesem Zusammenhang zeigt sich die Problematik fermatscher Pseudoprimzahlen: sie werden von einem Primzahltest, der den kleinen Satz von Fermat nutzt (Fermatscher Primzahltest), fälschlicherweise für Primzahlen gehalten. Wenn allerdings ein Verschlüsselungsverfahren wie RSA eine zusammengesetzte Zahl statt einer Primzahl verwendet, ist die Verschlüsselung nicht mehr sicher. Deshalb müssen bei solchen Verfahren bessere Primzahltests verwendet werden.

Euler und das Legendre-Symbol

Eine einfache Folge aus dem kleinen Satz von Fermat ist die folgende Aussage: Für jede ungerade Primzahl <math>p</math> und jede ganze Zahl <math>a</math>, die nicht durch <math>p</math> teilbar ist, gilt entweder

<math>a^{\frac{p-1}{2}} \equiv 1 \mod p</math>

oder

<math>a^{\frac{p-1}{2}} \equiv -1 \mod p.</math>

Man kann zeigen, dass der erste Fall genau dann eintritt, wenn es eine Quadratzahl <math>m^2</math> gibt, die kongruent zu <math>a</math> modulo <math>p</math> ist, siehe Legendre-Symbol.

Binomialkoeffizient

Für Primzahlen <math>p</math> und <math>1\leq k < p</math> gilt

<math>p\,\Big|{p\choose k};</math>

zusammen mit dem binomischen Satz folgt daraus

<math>(a+b)^p\equiv a^p+b^p\mod p.</math>

Für ganze Zahlen <math>a, b</math> folgt diese Aussage auch direkt aus dem kleinen fermatschen Satz, aber sie ist beispielsweise auch für Polynome mit ganzzahligen Koeffizienten anwendbar; im allgemeinen Kontext entspricht sie der Tatsache, dass die Abbildung <math>x\mapsto x^p</math> in Ringen der Charakteristik <math>p</math> ein Homomorphismus ist, der sogenannte Frobenius-Homomorphismus.

Aus dem Satz von Wilson (p ist genau dann eine Primzahl, wenn <math>(p-1)! \equiv -1 \pmod p</math> ist) folgt, dass für jede Primzahl p und jede natürliche Zahl n die Kongruenz

<math>{{np-1}\choose{p-1}} \equiv 1 \pmod{p}</math>

erfüllt ist.

Charles Babbage bewies 1819, dass für jede Primzahl p > 2 diese Kongruenz gilt:

<math>{{2p-1}\choose{p-1}} \equiv 1 \pmod{p^2}</math>

Der Mathematiker Joseph Wolstenholme (1829–1891) bewies dann 1862, dass für jede Primzahl p > 3 die folgende Kongruenz gilt:

<math>{{2p-1}\choose{p-1}} \equiv 1 \pmod{p^3}</math>

Giuga

Aus dem kleinen Satz von Fermat folgt, dass für eine Primzahl p gilt:

<math>1^{p-1} + 2^{p-1} + \dotsb + (p-1)^{p-1} \equiv -1 \pmod{p}</math>

Beispiel <math>p = 5</math>:

<math>1^4 + 2^4 + 3^4 + 4^4 = 1 + 16 + 81 + 256 = 354 = 71\cdot 5 - 1\equiv -1 \pmod{5}</math>

Giuseppe Giuga vermutete, dass auch die umgekehrte Schlussrichtung gilt, dass also eine Zahl mit dieser Eigenschaft stets prim ist. Es ist nicht geklärt, ob diese Vermutung richtig ist. Bekannt ist aber, dass ein Gegenbeispiel mehr als 10.000 Dezimalstellen haben müsste. Im Zusammenhang mit Giugas Vermutung werden die Giuga-Zahlen untersucht.

Lineare Rekursionen

Den kleinen fermatschen Satz kann man auch in der Form lesen: In der Folge <math>a^n-a</math> ist das <math>p</math>-te Folgenglied für eine Primzahl <math>p</math> stets durch <math>p</math> teilbar. Ähnliche Eigenschaften besitzen auch andere Folgen von exponentiellem Charakter, wie die Lucas-Folge (<math>p\mid L_p-1</math>) und die Perrin-Folge (<math>p\mid P_p</math>). Für andere lineare Rekursionen gelten analoge, aber kompliziertere Aussagen, beispielsweise für die Fibonacci-Folge <math>(f_n)_{n=0, 1, 2, \dotsc} = 0, 1, 1, 2, 3, 5, \dotsc</math>: Ist <math>p</math> eine Primzahl, so ist <math>f_p-\Big(\frac p5\Big)</math> durch <math>p</math> teilbar; dabei ist

<math>\Big(\frac p5\Big)=\begin{cases}1&p\equiv 1,4\mod 5\\-1&p\equiv2,3\mod 5\\0&p=5\end{cases}</math>

das Legendre-Symbol.

Divergenz der Summe der Kehrwerte

Die Reihe der Kehrwerte der Primzahlen ist divergent. Somit gilt:

<math>\sum_{i=1}^\infty \frac{1}{p_i} = \frac{1}{2} + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{11} + \dotsb = \infty</math>.

Das ist gleichbedeutend mit der Aussage, dass die durch <math>\textstyle a_n = \sum_{i=1}^{n} \frac{1}{p_i}</math> definierte Folge keinen endlichen Grenzwert besitzt, was wiederum bedeutet, dass sich für ein genügend groß gewähltes n jede erdenkliche reelle Zahl übertreffen lässt. Dies ist zunächst einmal verblüffend, da die Primzahllücken im Schnitt immer weiter zunehmen. Der Satz von Mertens trifft eine Aussage über das genaue Wachstumsverhalten dieser divergenten Reihe.

Primzahltests

Ob eine beliebige natürliche Zahl prim ist, kann mit einem Primzahltest herausgefunden werden. Es gibt mehrere solcher Verfahren, die sich auf besondere Eigenschaften von Primzahlen stützen. In der Praxis wird der Miller-Rabin-Test am häufigsten verwendet, der eine extrem kurze Laufzeit hat, allerdings mit kleiner Wahrscheinlichkeit falsch-positive Ergebnisse liefert. Mit dem AKS-Primzahltest ist es möglich, über die Primalität in polynomialer Laufzeit zu entscheiden. Allerdings ist er in der Praxis deutlich langsamer als der Miller-Rabin-Test.

Primzahlzertifikat

Herauszufinden, ob eine natürliche Zahl prim ist oder nicht, kann sehr aufwändig sein. Zu jeder Primzahl lässt sich aber eine Kette von Behauptungen angeben, die alle unmittelbar nachvollziehbar sind, zusammen die Primalität belegen und deren Gesamtlänge höchstens proportional ist zum Quadrat der Länge der Primzahl. Ein solcher Beleg wird Zertifikat (engl. primality certificate) genannt.

Bei der Zusammengesetztheit (Nichtprimalität) einer Zahl ist der Unterschied zwischen Beleg und Finden eines Belegs noch augenfälliger: Als Beleg genügen zwei Faktoren, deren Produkt die zusammengesetzte Zahl ergibt; das Finden eines echten Teilers kann aber sehr viel Aufwand bedeuten.

Größte bekannte Primzahl

Der Grieche Euklid hat im vierten Jahrhundert vor Christus logisch geschlussfolgert, dass es unendlich viele Primzahlen gibt; diese Aussage wird als Satz von Euklid bezeichnet. Euklid führte einen Widerspruchsbeweis für die Richtigkeit dieses Satzes (Elemente, Buch IX, § 20): Ausgehend von der Annahme, dass es nur endlich viele Primzahlen gibt, lässt sich eine weitere Zahl konstruieren, die eine bisher nicht bekannte Primzahl als Teiler hat oder selbst eine Primzahl ist, was einen Widerspruch zur Annahme darstellt. Somit kann eine endliche Menge niemals alle Primzahlen enthalten, also gibt es unendlich viele. Heute kennt man eine ganze Reihe von Beweisen für den Satz von Euklid.

Der Satz von Euklid besagt, dass es keine größte Primzahl gibt. Es ist jedoch kein Verfahren bekannt, das effizient beliebig große Primzahlen generiert – deshalb gab es stets eine jeweils größte bekannte Primzahl, seitdem sich die Menschen mit Primzahlen befassen. Derzeit (Stand: April 2017) ist es <math>2^{74.207.281}-1,</math> eine Zahl mit 22.338.618 (dezimalen) Stellen, die am 7. Januar 2016 mit einem CPU-Cluster der mathematischen Fakultät an der University of Central Missouri berechnet wurde. Für den Entdecker Curtis Cooper gab es für den Fund 3.000 US-Dollar vom Projekt Great Internet Mersenne Prime Search, das Mersenne-Primzahlen mittels verteiltem Rechnen sucht.

Die größte bekannte Primzahl war fast immer eine Mersenne-Primzahl, also von der Form <math>2^n-1,</math> da in diesem Spezialfall der Lucas-Lehmer-Test angewendet werden kann, ein im Vergleich zur allgemeinen Situation sehr schneller Primzahltest. Bei der Suche nach großen Primzahlen werden deshalb nur Zahlen dieses oder eines ähnlich geeigneten Typs auf Primalität untersucht.

Liste der Rekordprimzahlen nach Jahren

Zahl	Anzahl der Dezimalziffern	Jahr	Entdecker (genutzter Computer)
217−1	6	1588	Cataldi
219−1	6	1588	Cataldi
231−1	10	1772	Euler
(259−1)/179951	13	1867	Landry
2127−1	39	1876	Lucas
(2148+1)/17	44	1951	Ferrier
180·(2127−1)2+1	79	1951	Miller & Wheeler (EDSAC1)
2521−1	157	1952	Robinson (SWAC)
2607−1	183	1952	Robinson (SWAC)
21.279−1	386	1952	Robinson (SWAC)
22.203−1	664	1952	Robinson (SWAC)
22.281−1	687	1952	Robinson (SWAC)
23.217−1	969	1957	Riesel (BESK)
24.423−1	1.332	1961	Hurwitz (IBM7090)
29.689−1	2.917	1963	Gillies (ILLIAC 2)
29.941−1	2.993	1963	Gillies (ILLIAC 2)
211.213−1	3.376	1963	Gillies (ILLIAC 2)
219.937−1	6.002	1971	Tuckerman (IBM360/91)
221.701−1	6.533	1978	Noll & Nickel (CDC Cyber 174)
223.209−1	6.987	1979	Noll (CDC Cyber 174)
244.497−1	13.395	1979	Nelson & Slowinski (Cray 1)
286.243−1	25.962	1982	Slowinski (Cray 1)
2132.049−1	39.751	1983	Slowinski (Cray X-MP)
2216.091−1	65.050	1985	Slowinski (Cray X-MP/24)
391581·2216.193−1	65.087	1989	„Amdahler Sechs“ (Amdahl 1200)
2756.839−1	227.832	1992	Slowinski & Gage (Cray 2)
2859.433−1	258.716	1994	Slowinski & Gage (Cray C90)
21.257.787−1	378.632	1996	Slowinski & Gage (Cray T94)
21.398.269−1	420.921	1996	Armengaud, Woltman (GIMPS, Pentium 90 MHz)
22.976.221−1	895.932	1997	Spence, Woltman (GIMPS, Pentium 100 MHz)
23.021.377−1	909.526	1998	Clarkson, Woltman, Kurowski (GIMPS, Pentium 200 MHz)
26.972.593−1	2.098.960	1999	Hajratwala, Woltman, Kurowski (GIMPS, Pentium 350 MHz)
213.466.917−1	4.053.946	2001	Cameron, Woltman, Kurowski (GIMPS, Athlon 800 MHz)
220.996.011−1	6.320.430	2003	Shafer (GIMPS, Pentium 4 2 GHz)
224.036.583−1	7.235.733	2004	Findley (GIMPS, Pentium 4 2,4 GHz)
225.964.951−1	7.816.230	2005	Nowak (GIMPS, Pentium 4 2,4 GHz)
230.402.457−1	9.152.052	2005	Cooper, Boone (GIMPS, Pentium 4 3 GHz)
232.582.657−1	9.808.358	2006	Cooper, Boone (GIMPS, Pentium 4 3 GHz)
243.112.609−1	12.978.189	2008	Smith, Woltman, Kurowski et al. (GIMPS, Core 2 Duo 2,4 GHz)
257.885.161−1	17.425.170	2013	Cooper, Woltman, Kurowski et al. (GIMPS)
274.207.281−1	22.338.618	2016	Cooper, Woltman, Kurowski et al. (GIMPS)

Verteilung und Wachstum

Pi-Funktion und Primzahlsatz

In der Grafik wird die π-Funktion in blau dargestellt. Die Funktion n/ln(n) in grün und der Integrallogarithmus Li(n) in rot sind Approximationen der π-Funktion.

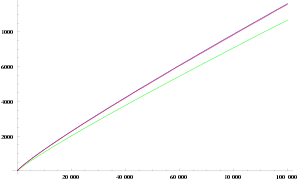
Zur Untersuchung der Verteilung der Primzahlen betrachtet man unter anderem die Funktion

<math>\pi \colon \Bbb N\to \Bbb N,\;n\mapsto\pi(n)</math>,

die die Anzahl der Primzahlen <math>\leq n</math> angibt und auch Primzahlzählfunktion genannt wird. Zum Beispiel ist

<math>\pi(1)=0\ ;\ \pi(10) = 4\ ;\ \pi(100) = 25\ ;\ \pi(1000) = 168; \ \pi(1000000)=78498</math>.

Diese Funktion und ihr Wachstumsverhalten ist ein beliebter Forschungsgegenstand in der Zahlentheorie. Mit der Zeit wurden einige Näherungsformeln entwickelt und verbessert.

Der Primzahlsatz besagt, dass

<math>\pi(x) \sim \frac{x}{\ln x}</math>

gilt, das heißt, dass der Quotient von linker und rechter Seite für <math>x\to\infty</math> gegen 1 strebt:

<math>\lim_{x \to \infty} \frac{\pi(x)} {\frac{x}{\ln x}} = 1</math> (siehe Asymptotische Analyse)

Der dirichletsche Primzahlsatz dagegen schränkt die Betrachtung auf Restklassen ein: Es sei <math>m</math> eine natürliche Zahl. Ist <math>a</math> eine ganze Zahl, die zu <math>m</math> nicht teilerfremd ist, so kann die arithmetische Folge

<math>a, a+m, a+2m, a+3m, \dotsc</math>

höchstens eine Primzahl enthalten, weil alle Folgenglieder durch den größten gemeinsamen Teiler von <math>a</math> und <math>m</math> teilbar sind. Ist <math>a</math> aber teilerfremd zu <math>m</math>, so besagt der dirichletsche Primzahlsatz, dass die Folge unendlich viele Primzahlen enthält. Beispielsweise gibt es unendlich viele Primzahlen der Form <math>4k+1</math> und unendlich viele der Form <math>4k+3</math> (<math>k</math> durchläuft jeweils die nichtnegativen natürlichen Zahlen).

Diese Aussage kann noch in der folgenden Form präzisiert werden: Es gilt

<math>\lim_{x\to\infty}\frac{\#\{p \ \mid \ \mathrm{prim},\ p\leq x\ \mathrm{und}\ p\equiv a\pmod m\}}{\#\{p \ \mid \ \mathrm{prim},\ p\leq x\}}=\frac1{\varphi(m)};</math>

dabei ist <math>\varphi(m)</math> die eulersche Phi-Funktion. In diesem Sinne liegen also für ein festes <math>m</math> in den Restklassen <math>a+m\mathbb Z</math> mit <math>\mathrm{ggT}(a,m)=1</math> jeweils „gleich viele“ Primzahlen.

Schranken

Die (bewiesene) Bonsesche Ungleichung garantiert, dass das Quadrat einer Primzahl kleiner ist als das Produkt aller kleineren Primzahlen (ab der fünften Primzahl).

Nach der (unbewiesenen) Andricaschen Vermutung ist die Differenz der Wurzeln der <math>n</math>-ten und der <math>(n+1)</math>-ten Primzahl kleiner als 1.

Primzahllücken

Die Differenz zwischen zwei benachbarten Primzahlen heißt Primzahllücke. Diese Differenz schwankt, und es gibt Primzahllücken beliebiger Größe. Es gibt aber auch Beschränkungen für die Lückengröße in Abhängigkeit von ihrer Lage:

Der Satz von Bertrand sichert die Existenz einer Primzahl zwischen jeder natürlichen Zahl <math>n</math> und ihrem Doppelten <math>2n</math>.

Nach der (unbewiesenen) Legendreschen Vermutung gibt es stets mindestens eine Primzahl zwischen <math>n^2</math> und <math>(n+1)^2</math>.

Abschätzungen zu Primzahlen und Folgerungen aus dem Primzahlsatz

Im Folgenden sei die Folge der Primzahlen mit <math>(p_n)_{n \in \N}</math> bezeichnet.

Abschätzungen

Für Indizes <math>n \in \N</math> gelten folgende Abschätzungen:

(1a)

<math>p_n < p_{n+1} < 2 \cdot p_n</math>

(1b)

<math>{p_{n+1}}^2 < 2 \cdot {p_n}^2</math> für <math>n \ge 5</math>

(1c)

<math>p_n < 2^n</math> für <math>n \ge 2</math>

(1d)

<math>p_n > n \cdot \ln(n)</math>

(1e)

<math>\sum_{k=2}^n{\frac{1}{p_k}} > \frac{1}{36} \cdot {\ln{\ln (n+1)}}</math> für <math>n \ge 2</math>

Folgerungen aus dem Primzahlsatz

Mit dem Primzahlsatz ergeben sich folgende Resultate:

(2a)

<math>\lim_{n \rightarrow \infty} \frac{p_{n+1}}{p_n} = 1</math>

(2b)

<math>\frac{n}{\ln(n) - \frac{1}{2}} < \pi(n) < \frac{n}{\ln(n) - \frac{3}{2}}</math> für <math>n \ge 67</math>

(2c)

Für jede positive reelle Zahl <math>x</math> existiert eine Folge <math>(q_n)_{n \in \N}</math> von Primzahlen mit

<math>\lim_{n \rightarrow \infty} \frac{q_n}{n} = x</math>.

(2d)

Die Menge der aus allen Primzahlen gebildeten Quotienten ist eine dichte Teilmenge der Menge aller positiven reellen Zahlen. D. h.: Für beliebige positive reelle Zahlen <math>a, b</math> mit <math>0 < a < b</math> existieren stets Primzahlen <math>p, q</math>, sodass

<math>a < \frac{p}{q} < b</math>

erfüllt ist.

Generierung von Primzahlen

Veranschaulichung des Algorithmus Sieb des Eratosthenes

Einer der ältesten Algorithmen zur Bestimmung von Primzahlen ist das Sieb des Eratosthenes. Bis heute ist kein effizienter Primzahlgenerator bekannt. Es gibt allerdings Formeln, bei denen eine gewisse Wahrscheinlichkeit besteht, dass die erzeugten Zahlen prim sind. Solche Zahlen müssen nachträglich noch auf ihre Primalität getestet werden.

Spezielle Primzahlen und Primzahlkonstellationen

• Cullen- und Woodall-Zahlen
• Cunningham-Ketten
• Elitäre Primzahlen
• Fastprimzahlen
• glückliche Primzahlen
• Gute Primzahlen
• Mersenne-Primzahlen
• Mills-Primzahlen
• Pierpont-Primzahlen
• Primzahlencousin
• Primzahltupel
• Primzahlzwillinge
• Prothsche Primzahlen
• Schwache Primzahlen
• Sexy Primzahlen
• Sophie-Germain-Primzahlen
• Streng nicht-palindromische Zahlen
• Ulam-Spirale
• Wall-Sun-Sun-Primzahlen

Weitere spezielle Arten von Primzahlen finden sich in der Kategorie:Primzahl.

Verallgemeinerung

In der Ringtheorie wird das Konzept der Primzahl auf die Elemente eines beliebigen kommutativen unitären Rings verallgemeinert. Die entsprechenden Begriffe sind Primelement und irreduzibles Element.

Die Primzahlen und deren Negative sind dann genau die Primelemente und auch genau die irreduziblen Elemente des Rings der ganzen Zahlen. In faktoriellen Ringen, das sind Ringe mit eindeutiger Primfaktorisierung, fallen die Begriffe Primelement und irreduzibles Element zusammen; im Allgemeinen ist die Menge der Primelemente jedoch nur eine Teilmenge der Menge der irreduziblen Elemente.

Insbesondere im zahlentheoretisch bedeutsamen Fall der Dedekindringe übernehmen Primideale die Rolle der Primzahlen.

Primzahlen in der Natur

In Nordamerika weisen manche Zikadenarten einen besonders langen Fortpflanzungsrhythmus von genau 13 oder 17 Jahren auf, mit dem sie den 2-, 4- und 6-jährigen Entwicklungsrhythmen ihrer Fressfeinde ausweichen.

Siehe auch

• Gilbreaths Vermutung
• Illegale Primzahl
• Permutierbare Primzahl
• Relativ prim

Literatur

• Peter Bundschuh: Einführung in die Zahlentheorie. 6. Auflage. Springer, Berlin 2008, ISBN 978-3-540-76490-8.
• Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. Beck, München 2004, ISBN 3-406-52320-X.
• Władysław Narkiewicz: The Development of Prime Number Theory. From Euclid to Hardy and Littlewood. Springer, Berlin 2000, ISBN 3-540-66289-8.
• Paulo Ribenboim: The New Book of Prime Number Records. Springer, New York 1996, ISBN 0-387-94457-5.

• Robert E. Dressler, Louis Pigno, Robert Young: Sums of squares of primes. In: Nordisk Mat. Tidskr. Band 24, 1976, S. 39–40 (MR0419352). 
• Hans Rademacher, Otto Toeplitz: Von Zahlen und Figuren. Proben mathematischen Denkens für Liebhaber der Mathematik (= Heidelberger Taschenbücher. Band 50). Springer Verlag, Berlin (u. a.) 1968 (MR0252141). 
• J. B. Rosser: The n-th prime is greater than n log n. In: Proc. London Math. Soc. Band 45, 1939, S. 21–44. 
• J. Barkley Rosser, L. Schoenfeld: Approximate formulas for some functions of prime numbers. In: Illinois J. Math. Band 6, 1962, S. 64–94 (projecteuclid.org [PDF]).  MR0137689
• Wacław Sierpiński: Elementary Theory of Numbers (= North-Holland Mathematical Library. Band 31). 2. überarbeitete und erweiterte Auflage. North-Holland (u. a.), Amsterdam (u. a.) 1988, ISBN 0-444-86662-0. 
• József Sándor, Dragoslav S. Mitrinović, Borislav Crstici: Handbook of Number Theory. 2. Auflage. Band I. Springer-Verlag, Dordrecht, NL 2006, ISBN 978-1-4020-4215-7 (MR2186914). 

Externe Links

 Commons: Primzahlen – Sammlung von Bildern, Videos und Audiodateien

 Wiktionary: Primzahl – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

 Wikibooks: Fundamentalsatz der Arithmetik – Lern- und Lehrmaterialien

 Wikibooks: Primzahlen von 2 bis 100.000 – Lern- und Lehrmaterialien

• The Prime Pages (englisch)
• Die Primzahlenseite
• Eric W. Weisstein: Rosser’s Theorem. In: MathWorld (englisch).
• Liste der Primzahlen zwischen 1 und 1.000.000